两种搜索算法

今天来讲一下常见的两种算法：广度优先搜索和深度优先搜索

这两种算法呢各自都有自己的特点，下面我来详细的解析一下

1.广度优先算法

广度优先算法，顾名思义，广度优先，他是在借助队列的情况下，通过不停的切换起点来对树进行搜索为了给大家解释这个问题，我找来了一棵树

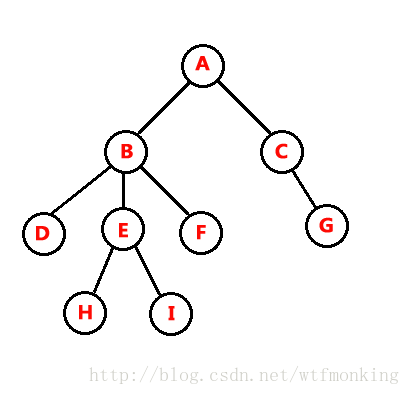
假如我们以A作为起点，以H作为终点，于是，我们把目光投降A，我们先把A加入队列中，然后我们检查与A相连的节点，发现A与B，C相连，于是我们将A从队列中移除，将B，C加入队列中

按照广度优先找起点的原则，我们现在要找一个新的起点，那我们找哪个起点合适呢？很显然，因为队列只能找到队首的那个元素，所以B理所当然的成为了新的起点，接着，我们将B弹出

再来看看有哪些是时与B相连的，于是我们找到了A，D，E，F四个点，因为A已经被搜索过一次了，所以不能将A加入队列

我们将D，E，F三个点加入队列中。然后我们再把队列的首元素拿出来，这次我们该从C开始搜索了，我们先弹出C，C下面只有一个G，于是我们把G放入队列中。

然后我们再来看，从队首取出D并且将D弹出，因为D下面已经没有节点了，所以A-->B-->D这一条线就搜索完了，我们再拿出队首的元素E并将其弹出，将其下H，I两个节点加入队列中，以此类推，当队列中的元素都为空是，就表示我们遍历了整个树，这就是广度优先算法的大致思路，

总结一下大致思路：

找到起点-->弹出起点-->找到相邻节点（未被搜索过）-->将节点加入队列中-->从队列中取出新的节点-->弹出节点……

来看看例题：NOJ P1663

这个题便是典型的广搜题，其实理论深搜也能写，但是超时的可能性应该比较大，毕竟n都取到200了

下面来看看AC代码：

#include <bits/stdc++.h>
using namespace std;
struct node{
    int x,cnt;//x用来存储起点，cnt用来存储步数
};
queue<node>q;
int location[205][205],vis[205];//vis用于标记已经搜索过的节点
int main(){
    int n,be,en;
    cin>>n>>be>>en;
    for (int i=1;i<=n;i++){
        for (int j=1;j<=n;j++){
            cin>>location[i][j];
        }
    }
    q.push({be,0});//将起点放入队列中
    vis[be]=1;//标记节点
    while (!q.empty()){
        int x=q.front().x;//当前的起点
        int cnt=q.front().cnt;//搜索的第cnt步，cnt-1就是经过的多少人
        q.pop();//千万不要忘了将当前起点弹出
        if (en==x) {
            cout<<cnt-1<<endl;
            break;
        }
        for (int i=1;i<=n;i++){
            if (location[x][i]&&vis[i]==0){
                vis[i]=1;
                q.push({i,cnt+1});//找打下一个节点并将其放入队列中
            }
        }
    }
    return 0;
}

2.深度优先算法

与广度优先算法不同，深度优先算法讲究的是一条道走到黑，并且搜索完一整条路径之后会通过回溯的方式寻找未访问过的节点，并以此进入下一条道

深搜的题一般都和递归有关系所以初学的时候看起来会比较难懂

下面我用刚刚的那棵树再解释一下：

假如我们以A作为起点，于是，我们现在有两种选择：1.搜索B，2.搜索C。

我们定如下规则，优先搜索左边的内容。那么我们就应该搜索B，再看看B，与其连接的有三个点：A，D，E，F，因为A已经被搜索过了，我们便忽略A

按照规则，我们现在搜索D，我们发现，D已经没有路可走了，路线A-->B-->D已经走到了尽头，于是我们开始回溯，我们从B节点开始搜素E……以此类推，当我们搜到H时，又开始回溯，通过不停的执行这种过程，我们便可以将整棵树完全访问，这便是深度优先搜索的大致原理

总结一下大致思路：

从起点开始搜索-->依次寻找下一个优先节点-->到达路径末尾-->开始回溯到最近一个没有被访问的节点-->继续搜索……

我们来看一下深搜的模板吧：

void DFS(int cur)
{
    if(满足所需要的条件){
        相应的操作；
           return；
    }
    //这里对应一个递归的基，就是开始返回的地方
    else{
        for(int i= ; ;) //如果是方向的话，会枚举方向
        {
            枚举加方向的新坐标；
            if(界限 ：例如：不能出到地图外，有障碍，已经访问过)
                continue;
               设置已经访问新坐标；
            DFS(新坐标); 
            恢复到未被访问；
        }
    }
}  

int main()
{
    dfs(0)//从某个起点开始搜索
} 

其实大部分的深搜都是这个样子，但是还是得学会灵活变通

例题：
洛谷P2089 烤鸡
洛谷P1219 八皇后