KMP算法的实现及其优化

于2020.4.8日重写

kmp算法的实现有多种方式，我这里讲两种：
传统写法以及确定有限状态机版
有限状态机版待修改

kmp算法简介

KMP 算法是一种改进的字符串匹配算法，由 D.E.Knuth，J.H.Morris 和 V.R.Pratt 提出的，因此人们称它为克努特 — 莫里斯 — 普拉特操作（简称 KMP 算法）。KMP 算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 next () 函数实现，函数本身包含了模式串的局部匹配信息。KMP 算法的时间复杂度 O(m+n)。 ——摘自百度百科

在普通的字符串匹配算法中，我们可能会使用两个for循环来不停的匹配字符串，直到完全匹配完为止，就是类似于如下的一种写法：

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-08 13:43:16
 * @Website1: 449293786.site
 */
#include<bits/stdc++.h>
using namespace std;
int search(string cmp,string pattern)
{
    int i=0,j=0;
    while (i<cmp.length()&&j<pattern.length())
    {
        if (cmp[i]==pattern[j])
        {
            i++,j++;
        }
        else
        {
            i=i-j+1;
            j=0;
        }
    }
    if (j=pattern.length())
    {
        return i-j+1;
    }
    return -1;
}
int main()
{
    string cmp,pattern;
    cin>>cmp>>pattern;
    cout<<search(cmp,pattern)<<endl;
    return 0;
}

这就是比较常用的幼稚算法，时间复杂度差不多O(n^2)，用的也比较广，如果没有记错的话，java内置的find()函数好像也是用这样实现的……对此我不做任何评价

一、传统写法

然后是kmp算法的传统写法，这个算法的核心就是利用模式字符串pattern求出一个next数组，然后利用这个数组进行匹配，优点是待匹配字符串不必再回溯，可以直接扫描一遍就过，时间复杂度为O(n)，具体工作方式如下图

从图中我们可以看出，i指针并没有回退，而是一次性扫描就结束，利用已经部分匹配的这个有效信息，保持i指针不回溯，通过修改模式字符串指针，让模式字符串尽量移动到有效的位置，这也正是kmp算法的神奇之处。

我们先抛开复杂的next数组，首先看看匹配函数

search()函数

search函数和暴力写法比较类似

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-08 13:10:56
 * @Website1: 449293786.site
 */
int search(string cmp, string pattern)
{ 
    if(pattern == "") 
        return 0; 
    int* next = get_next(pattern);
    int i=0;//待匹配字符串指针
    int j=0;//模式字符串指针
    while(i <cmp.length() && j <pattern.length())
    {
        if(j == -1 || cmp[i] == pattern[j])
        {
            i++;j++;
            //匹配成功或者模式指针被回退到了-1
        }
        else
        {
            j = next[j];
            //匹配失败，模式指针回退到next[j]
        }
    }
    if(j == pattern.length())
    {
        //模式指针走完全程，匹配成功
        return i-j; 
    }
    else
    {
        //匹配失败，返回-1
        return -1; 
    }
}

或许你看了代码又开始疑惑了，这next数组是啥呢？它咋知道该回退到哪个位置呢？不要心急，待我慢慢道来

next数组

这里我们先做一个约定：

i为待匹配字符串指针，j为模式字符串指针

这个数组是为了实现让待匹配字符串指针不回溯，只让模式字符串指针回退的工具，也是kmp算法最核心的部分，很多的算法书在这里都是一笔带过，确实让读者比较难受，所以我决定这里讲细一点

next数组记录了啥？

确切的来说，next数组记录的是这个字符失配后，模式字符串指针应当回退到的位置

next数组怎么计算？

我们先来观察一下kmp算法的匹配规律

情形1：

在CD时发生了失配，于是j开始回溯

回溯后继续开始匹配

情形2：

在CD时发生失配

开始回溯

我们仔细观察一下两种情形：
情形1中发生失配，j指针回溯到了1号位（从0号位开始）
情形2中发生失配，j指针回溯到了2号位

那我们猜想，是不是和模式字符串中的什么东西有关呢？凭借这种猜想，我们来观察一下两个模式字符串：
ABAD，其中发生失配的D前面，有ABA，其中A和A是一样的，长度为1
ABCABB，其中发生失配的B前面，有ABCAB，其中AB和AB是一样的，长度为2

我们把相同的这一段分别叫做公共前缀和公共后缀，而失配后回溯的位置刚好是公共前后缀的长度

我们规定零号为上的值为-1，利用这个性质，我们可以来试着求一下next数组

假如有如下pattern（模式）字符串：

ABABABB -> -1 0 0 1 2 3 4
ABAB -> -1 0 0 1
AAAB -> -1 0 1 2

接下来的问题就是如何利用代码计算next数组了

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-08 14:52:57
 * @Website1: 449293786.site
 */
#include <bits/stdc++.h>
using namespace std;
int* get_next(string pattern)
{
    int* next = new int[pattern.length()];
    //动态申请一段空间
    next[0] = -1;
    //将next数组初始化
    int i = 0;//模式字符串指针
    int k = -1;//记录最大公共前缀长度
    int size = pattern.length();
    while(i<size - 1)
    {
        if(k == -1 || pattern[k] == pattern[i])
        {
            //如果匹配上了，公共前缀长度增加
            i++;k++; next[i] = k;
        }
        else
        {
            //如果失配了，改变公共前缀的长度
            k = next[k];
        }
    }
    return next;
}

int main()
{
    string pattern;
    cin>>pattern;
    int *next=get_next(pattern);
    for (int i=0;i<pattern.length();i++)
    {
        cout<<next[i]<<" ";
    }
    return 0;
}

这里再解释一下k=next[k]

当我们找不到abab这个最大的后缀串的时候，我们可以找到ab，b这样的前缀串，这个过程就可以直接从next[k]里面取得

传统版本代码：

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-09 09:39:32
 * @Website1: 449293786.site
 */
#include <bits/stdc++.h>
using namespace std;
int* get_next(string pattern)
{
    int* next = new int[pattern.length()];
    next[0] = -1;
    int j = 0;
    int k = -1;
    int size = pattern.length();
    while(j<size - 1)
    {
        if(k == -1 || pattern[k] == pattern[j])
        {
            j++;k++; next[j] = k;
        }
        else
        {
            k = next[k];
        }
    }
    return next;
}
int KMP(string cmp, string pattern)
{
    if(pattern == "") return 0;
    int* next = get_next(pattern);
    int i=0;
    int j=0;
    while(i < int(cmp.length()) && (j < int(pattern.length())))
    {
        if(j == -1 || cmp[i] == pattern[j])
        {
            i++;j++;
        }
        else
        {
            j = next[j];
        }
    }
    if(j == pattern.length())
    {
        return i-j;
    }
    else
    {
        return -1;
    }
} 
int main()
{
    string cmp,pattern;
    cin>>cmp>>pattern;
    int location=KMP(cmp,pattern);
    cout<<location<<endl;
    return 0;
}

传统代码分析：

当出现如下情形的时候

这一步完全就没有意义了，因为CB是不能匹配的，所以我们添加一个判断条件：P[j] == P[next[j]]

传统代码升级版

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-08 12:31:30
 * @Website1: 449293786.site
 */
#include<bits/stdc++.h>
using namespace std;
int* get_next(string pattern)
{
    //get next array and return a point
    int size=pattern.length();
    int* next=new int[size];
    //动态申请一块空间
    next[0]=-1;
    //给零号位初始化为-1，当零号位不能匹配时整体后移一位
    int j=0,k=-1;
    while (j<pattern.length()-1)
    {
        if (k==-1||pattern[j]==pattern[k])
        {
            if (pattern[++j]==pattern[++k])
            {
                next[j]=next[k];
            }
            else next[j]=k;
        }
        else k=next[k];
    }
    return next;
}

int KMP(string cmp, string pattern)
{ 
    if(pattern == "") 
        return 0; 
    int* next = get_next(pattern);
    int i=0;
    int j=0; 
    int cnt=0;
    while(i < int(cmp.length()) && (j < int(pattern.length())))
    {
        if(j == -1 || cmp[i] == pattern[j])
        {
            i++;j++; 
        }
        else
        {
            j = next[j];
        }
        cnt++;
    }
    cout<<"cnt="<<cnt<<endl;
    if(j == pattern.length())
    {
        return i-j; 
    }
    else
    {
        return -1; 
    }
}

int main()
{
    string cmp,pattern;
    int number1,number2;
    cin>>cmp>>pattern;
    cout<<KMP(cmp,pattern);
    return 0;
}

二、确定有限状态机

说实话，这种算法严格意义上来说不应该是kmp算法，但是他的核心却又和kmp算法类似，里面又参和了点DP的味道，确实挺不错的，但是空间复杂度却比传统kmp算法大O(n^2)

先看一下这种算法的大概结构：

void get_next(string pattern)
{
    //通过pattern构建next数组
}
void kmp(string cmp)
{
    //借助next数组来匹配cmp
}

我先大致解释一下状态机：

在这张图里，圆圈内的数字就是状态，0是起始状态，5是终止状态，开始匹配时，pattern处于起始状态，一旦匹配到终止状态，就说明匹配成功

接下来我们看几个例子

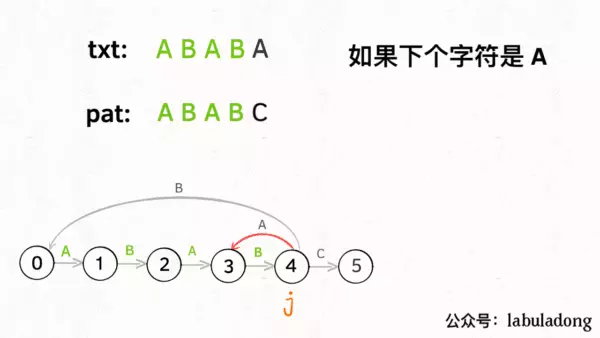
当待匹配字符串已经完成了ABAB四个字符的匹配，接下来的状态，是由待匹配字符串的下一位决定的

如果下一位是A，那么pattern就转换到状态3

如果下一位是B，就要打回去重新做人（我jojo不做人啦！！！）

如果下一位是C，那么就转移到状态5，即终止状态，字符串匹配完毕

当然，如果遇到的是其他字符，也应当转换到状态0去

然后，经过一系列神奇的变化，就有了：（怎么求接下来讲，小伙伴们不必心慌）

嗯……简直清晰……

再看看这种算法的核心，仔细理解这个图

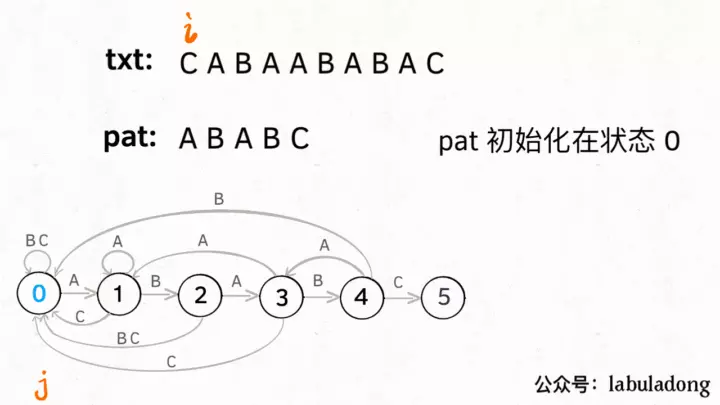
next数组怎么计算？

next[j][c]=next_status
0 <= j < M，代表当前的状态
0 <= c < 256，代表遇到的字符（ASCII 码）
0 <= next_status <= M，代表下一个状态

next[4]['A'] = 3 表示：
当前是状态 4，如果遇到字符 A，
patttern 应该转移到状态 3

next[1]['B'] = 2 表示：
当前是状态 1，如果遇到字符 B，
patttern 应该转移到状态 2

因为我们已经确定了next数组的含义，所以定义next数组的时候就有如下的框架：

for 0 <= j < M: # 状态
    for 0 <= c < 256: # 字符
        dp[j][c] = next

如果遇到的字符能够和pattern[i]匹配，则状态向前推进
否则就保持原地不动或者回退，我们称为状态重启

状态重启↓↓↓

那么，怎么确定重启的位置呢？

这里要引进一个新的名词：影子状态
指的是和当前状态具有相同的前缀，（其实就类似于最大公共前缀和最大公共后缀了）

当前状态j=4，其影子状态为x=2，他们都有相同的前缀“AB"，因为状态x和j存在相同的前缀，所以，当状态j准备重启的时候，会来问问x，x会告诉他应该会到哪里

比如：当j遇到字符”A"，他应当转移重启到哪里呢？状态j回来问问x，就是next[j]['A']=next[x]['A'],而x中已经提前算好了应当回退到哪个位置

为什么呢？
kmp中，为了减少不必要的计算，j就应该去找和自己有相同前缀的x：如果x遇见“A”，该回退到哪个位置。这样转移过去，才能使回退最少，j只需要跟着x走就行了

接下来再细化一下代码框架：

int X # 影子状态
for 0 <= j < M:
    for 0 <= c < 256:
        if c == pat[j]:
            # 状态推进
            dp[j][c] = j + 1
        else: 
            # 状态重启
            # 委托 X 计算重启位置
            dp[j][c] = dp[X][c]

最后，给出确定有限状态机版本的方程：

/*
 * @Author: Mr.Sen
 * @LastEditTime: 2020-04-08 13:08:01
 * @Website1: 449293786.site
 */
#include<bits/stdc++.h>
using namespace std;
int next1[100][256];
void get_next(string pattern)
{
    int shadow=0;
    int size=pattern.length();
    next1[0][pattern[0]]=1;
    for (int i=1;i<size;i++)
    {
        for (int j=0;j<256;j++)
        {
            next1[i][j]=next1[shadow][j];
        }
        next1[i][pattern[i]]=i+1;
        shadow=next1[shadow][pattern[i]];
    }
}
int search(string cmp,string pattern)
{
    int size_pattern=pattern.length();
    int size_cmp=cmp.length();
    int j=0;
    for (int i=0;i<cmp.length();i++)
    {
        j=next1[j][cmp[i]];
        if (j==size_pattern)
            return i-size_pattern+1;
    }
    return -1;
}
int main()
{
    get_next("sip");
    cout<<search("missisasipi","sip");
    return 0;
}

难为死我了……

文章参考&图片来源（实在太懒不想自己手动画图……）：

https://zhuanlan.zhihu.com/p/83334559

https://www.cnblogs.com/yjiyjige/p/3263858.html